High Speed Fixed Point Division

to be published...

In this page you can found the VHDL codes, additional figures and more experimental data of the article:

High Speed Fixed Point Division in FPGA

Summary

This work propose dividers for fixed-point operands. The divider divides in a radix r = 2^k, producing k bits at each iteration. The proposed digit recurrence algorithm has two different architectures called arch1 and arch2. The first is for general hardware implementation, the second one is optimized for configurable logic (FPGAs). Preliminary results show a speedup greater to three times respect to a classical non-restoring division implemented in Xilinx Devices.

VHDL codes:

Sequential Implementations

* Sequential non-restoring. A sequential version of a base-2 non-restoring divider. For naturals of X-bits and Y-bits. The constant GRAIN defines the amount of bits computed at each cycle. The algorithm needs XBITS/GRAIN + 1 cycles to calculate the result.(div_nr_sec_behav.zip)

* Radix 4 with proposed arch 1, behavioral model (r4_a1 in paper uses slightly modifications) (div_sec_r4_arch1.rar).

* Radix 4 using proposed arch2, behavioral model (r4_a2 in paper uses slightly modifications) (div_sec_r4_arch2.rar).

* Radix 16 arch 2 low level (r16_a2_low in paper). (XST netlist, A VHDL to instantiate the netlist, A VHDL simulation model, a simple VHDL testbench, a text file with stimulus). This circuits uses low level component instantiation. If you need the VHDL models contact us.

     -  for 64 by 32 bit divisor (div_r16_a2_low64_32.rar)

      - for 256 by 128 bit divisor (div_r16_a2_low256_128.zip).

Pipelined Implementation

* Pipelined radix 4 arch2 divider, (pipe_r4_gX in paper) pipelining every GRAIN steps  (div_pipe_r4_arch2.rar).

* Pipeline non restoring low level implementation 32 by 32 bits operands (pipe_nr_low in paper) (XST netlist, A VHDL to instantiate the netlist, A VHDL simulation model, a simple VHDL testbench, a text file with stimulus). (div_nr_pipe_low.zip).

Combinational Implementation

* Combinational radix 4 arch2 divider, (comb_r4_a2) (div_comb_r4_arch2.rar).

More Divider models

From book "Synthesis of Arithmetic Circuits: FPGAs, ASICs and Embedded Systems", Deschamps/ Bioul / Sutter; John Wiley & Sons 2006, at http://www.arithmetic-circuits.org/arithmetic/vhdl_codes.htm

Additional Figures:

*Sequential Implementations of a radix 2^k divider

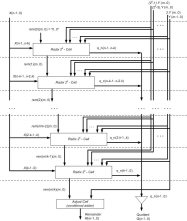
* Pipelined array for a radix 2^k divider. In the intersection between the doted line and interconection registers are used..

* Combinatiol array for a radix 2^k divider.

Radix 4(2^2) cell using arch1

Radix 8(2^3) cell using arch1

Radix 4(2^2) cell using arch2

Radix 16(2^3) cell using arch2

More Experimental Data:

Combinational Circuits 8 by 8, 16 by 16, and 32 by 32 (implement_comb.pdf)

32 bits by 32 bits dividers (implement_32by32.pdf)

256 by 128 bits divider (implement_seq256div128.pdf)

256 by 128 bits divider figure (fig_seq256div128.pdf)